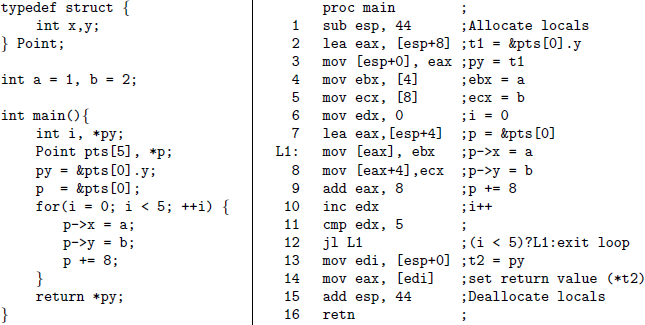
As I’ve written about recently, I’ve been hacking on VSA. I’ve been trying to get to the point where the example in Balakrishnan’s dissertation works. I chose this example because I don’t know of any others! Below is a snapshot of the example that I started with.

And here are the results that VSA is supposed to be able to infer:

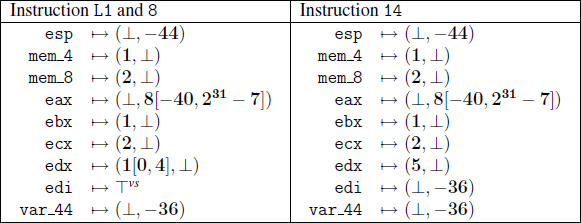
There are several interesting things about these results. First, note that %edx is bounded, even though it is incremented in a loop. In contrast, %eax grows to its maximum value. Although %eax approaches the maximum positive integer, VSA infers that it does not overflow. That sounds kind of weird, doesn’t it?

My VSA implementation does not yield the same results. It notices that %eax is incremented without a direct bound on line 9, and widens %eax to 2^31 - 8 at line 7. On line 9, the computation %eax + 8 overflows, and represents any value on the stack. The next loop iteration, we see weak updates to the whole stack at L1 and line 8, since %eax represents any stack address.

Somewhere there’s a hidden assumption in addition of value-sets that says adding values in non-global regions cannot overflow. This kind of makes sense, if regions are separated, since the program might crash. I do not consider this to be a sound assumption, however. (Programs can handle exceptions…) Perhaps that is why this assumption is not explicitly mentioned, or if it is, is so buried that I could not find it. I expected it to be in the definition of addition for value-sets, but it’s not there.

With this assumption/hack, we get the same results as the example above.