As I’ve written about recently, I’ve been hacking on VSA. I’ve been trying to get to the point where the example in Balakrishnan’s dissertation works. I chose this example because I don’t know of any others! Below is a snapshot of the example that I started with.

And here are the results that VSA is supposed to be able to infer:

There are several interesting things about these results. First, note that %edx is bounded, even though it is incremented in a loop. In contrast, %eax grows to its maximum value. Although %eax approaches the maximum positive integer, VSA infers that it does not overflow. That sounds kind of weird, doesn’t it?

My VSA implementation does not yield the same results. It notices that %eax is incremented without a direct bound on line 9, and widens %eax to 2^31 - 8 at line 7. On line 9, the computation %eax + 8 overflows, and represents any value on the stack. The next loop iteration, we see weak updates to the whole stack at L1 and line 8, since %eax represents any stack address.

Somewhere there’s a hidden assumption in addition of value-sets that says adding values in non-global regions cannot overflow. This kind of makes sense, if regions are separated, since the program might crash. I do not consider this to be a sound assumption, however. (Programs can handle exceptions…) Perhaps that is why this assumption is not explicitly mentioned, or if it is, is so buried that I could not find it. I expected it to be in the definition of addition for value-sets, but it’s not there.

With this assumption/hack, we get the same results as the example above.

I am a big believer in the appliation of semantics-based program analysis to binary analysis. In other words, I think that we should examine program semantics rather than program syntax. Syntax-oriented analyses operate at the assembly level, e.g.,

1

add %eax, %ebx

while semantics-oriented analyses look at a lifted form of assembly, like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

addr 0x0 @asm "add    %eax,%ebx"
label pc_0x0
T_t1:u32 = R_EBX:u32
T_t2:u32 = R_EAX:u32
R_EBX:u32 = R_EBX:u32 + T_t2:u32
R_CF:bool = R_EBX:u32 < T_t1:u32
R_AF:bool = 0x10:u32 == (0x10:u32 & (R_EBX:u32 ^ T_t1:u32 ^ T_t2:u32))
R_OF:bool = high:bool((T_t1:u32 ^ ~T_t2:u32) & (T_t1:u32 ^ R_EBX:u32))
R_PF:bool =
  ~low:bool(R_EBX:u32 >> 7:u32 ^ R_EBX:u32 >> 6:u32 ^ R_EBX:u32 >>
  5:u32 ^
            R_EBX:u32 >> 4:u32 ^ R_EBX:u32 >> 3:u32 ^ R_EBX:u32 >>
            2:u32 ^
            R_EBX:u32 >> 1:u32 ^ R_EBX:u32)
R_SF:bool = high:bool(R_EBX:u32)
R_ZF:bool = 0:u32 == R_EBX:u32

However, over the past few days, I’ve concluded that there are some cases in which it may be preferable to use syntax. To give you some perspective, I’ve been working on our VSA implementation, as I’ve described in my previous blog posts. One of the problems I have been working on is adding high level edge conditions at branch points.

What are high level edge conditions? Well, to really grok what that means, you need to see how BAP would model a branch. Let’s use the below program as an example, which merely does a compare and branch.

1
2

cmp %eax, %ebx
ja foo

Now, before we go further, stop and ask yourself “What is the high-level branch condition?” You probably just thought ebx > eax. And you’d be right! Let’s see what a semantics-oriented answer would be from BAP.

Here, the branch condition is ~(cf | zf). Gee, thanks BAP. If we apply copy propagation, which is essentially substitution, we get ~(ebx < eax | 0 == ebx - eax). Obviously, with a little simplification, this turns into ebx >= eax & ebx != eax, or ebx > eax.

My point here is that recovering the high-level condition is awkward. In semantics approaches, we lift from syntax to semantics, and yet to recover this high-level condition we are effectively undoing this transformation. I’ve seen this come up in a few places, with our VSA implementation only being the most recent.

It would be nice if there was a nice, principled way of recovering higher-level conditions. For example, if we could create a lattice that compares how “high level” expressions are, and automatically map an expression to a higher expression on the lattice, I’d feel much better about this problem. As things stand, I have defined a number of simplifications that get the job done, but they are somewhat specific to our lifting mechanism. If we change how we lift instructions, we could break the high-level condition recovery, which just seems ugly.

On the bright side, BAP’s VSA implementation is good enough to compute the target addresses of switch jump tables now. So hopefully tomorrow I’ll have CFG recovery at least partially working! Here’s the “new” version of the edge conditions for the above example:

It was a busy weekend. I competed with PPP in the 20th Defcon CTF. Unlike last year, I competed remotely from Pittsburgh. This year’s Defcon CTF ran much more smoothly than last year. PPP got 2nd place. We are disappointed we didn’t win, but we did pretty well. We only had about 12 people on our team. Someone said the winning team had about 50 people on it! Pretty crazy.

Anyway, I spent more time thinking about the VSA problem I posted about last time, and my conclusion is that SSA form can actually be harmful for abstract interpretation. In dataflow, the order vertices are visited in does not matter, since the solution to the dataflow should be the meet over all paths.

This property does not hold for abstract interpretation, and the final result can vary depending on the path taken. Converting to SSA form effectively changes the path taken by the abstract interpretation algorithm, so it should not be too surprising that we get a different answer.

I decided to deal with this by changing our VSA implementation to operate on non-SSA CFGs. This makes sense for VSA, but also for CFG recovery in general, since converting to SSA in a dynamic fashion seems difficult anyway.

Here’s the final result I get from VSA for my toy example:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

VSA @BB_Entry
 R_ESP_1:u32 -> (R_ESP_1:u32 |=> 0[0,0])

VSA @BB_Exit
 R_ESP_1:u32 -> (R_ESP_1:u32 |=> 0[0,0])
 x_81:u32 -> ($ |=> 1[1,3])

VSA @BB_Indirect

VSA @BB_Error

VSA @BB_0
 R_ESP_1:u32 -> (R_ESP_1:u32 |=> 0[0,0])
 x_81:u32 -> ($ |=> 0[0,0])

VSA @BB_1
 R_ESP_1:u32 -> (R_ESP_1:u32 |=> 0[0,0])
 x_81:u32 -> ($ |=> 1[1,3])

VSA @BB_2
 R_ESP_1:u32 -> (R_ESP_1:u32 |=> 0[0,0])
 x_81:u32 -> ($ |=> 1[1,3])

Here’s the CFG again for reference:

Good news and bad news. I’ve made more progress on BAP’s VSA implementation. Recall this example from last time:

BAP’s VSA now outputs this:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

VSA @BB_Entry
 R_ESP_1:u32 -> (R_ESP_1:u32 |=> 0[0,0])

VSA @BB_Exit
 R_ESP_1:u32 -> (R_ESP_1:u32 |=> 0[0,0])
 x_82:u32 -> ($ |=> 0[0,0])
 x_83:u32 -> VS.top
 x_84:u32 -> ($ |=> 1[4,2147483647])

VSA @BB_0
 R_ESP_1:u32 -> (R_ESP_1:u32 |=> 0[0,0])
 x_82:u32 -> ($ |=> 0[0,0])

VSA @BB_1
 R_ESP_1:u32 -> (R_ESP_1:u32 |=> 0[0,0])
 x_82:u32 -> ($ |=> 0[0,0])
 x_83:u32 -> ($ |=> 1[-2147483648,3])
 x_84:u32 -> ($ |=> 1[-2147483647,4])

VSA @BB_2
 R_ESP_1:u32 -> (R_ESP_1:u32 |=> 0[0,0])
 x_82:u32 -> ($ |=> 0[0,0])
 x_83:u32 -> VS.top
 x_84:u32 -> ($ |=> 1[4,2147483647])

There is something odd going on here. At BB_1, VSA determines that x_83 can be (almost) any number below 4. However, it’s obvious that x_83 cannot be negative.

What’s going on? Well, x_83 starts out as phi(x, x_84), which means that x_83 gets its value from either x or x_84, depending on control flow. Read up on SSA form if this makes no sense to you. VSA determines that x_83’s value set is the union of x and x_84’s value sets. Sounds good so far. x always has zero, so that one is easy. x_84 will initially be Top, since we have not seen an assignment for it yet. Since Top is any value, Top union anything is Top. Thus, x_83 becomes Top, and x_84 becomes Top + 1. Now, when the value set of x_84 flows through the edge condition x_84:u32 <= 3:u32, any values above 3 are removed, leaving us with (almost) any value less than 4.

VSA is an abstract interpretation algorithm, but not a dataflow algorithm. In dataflow problems, data values always move downward in the lattice. But in abstract interpretation, they can move up and down, which is what happens with VSA when we perform union (up) and intersection (down). I am used to working with dataflow problems, and so this seems very unnatural to me.

It seems like we would get the right answer if the initial lattice values of each node used the edge conditions somehow; right now the initial lattice values are simply Top. But if the initial lattice value for BB_1 had x_84 constrained to be less than 4, we’d get the right answer. It also seems like we would get the right answer if we were not using SSA. The original author of BAP VSA wrote it as an SSA analysis, although I do not know why. I do not think there is any benefit.

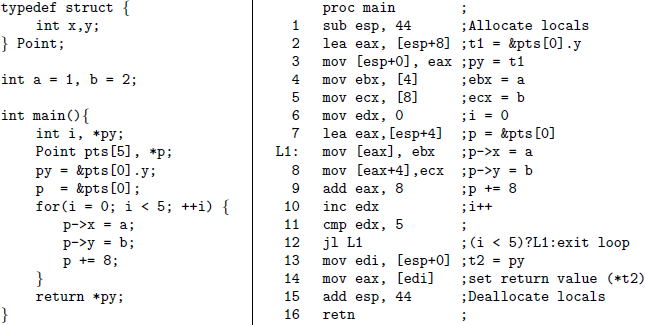
One of BAP’s biggest omissions is that it does not do CFG/code recovery. CFG recovery (or code recovery) is the process of finding what parts of an executable are code. If you have ever used IDA Pro, when you first load a file, the initial analysis phase is actually performing CFG recovery. For this, IDA Pro uses a combination of recursive disassembly (if address a is code and has jmp 1234, then 1234 must be code too) and heuristics like looking for push %ebp; mov %esp, %ebp.

A third approach to CFG recovery, besides recursive disassembly and heuristics, is abstract interpretation. Abstract interpretation is a method for analyzing programs in a sound way. One abstract interpretation algorithm for recovering CFGs is called Value Set Analysis, or VSA for short. VSA works by overapproximating the values of variables by using strided intervals. A strided interval is a combination of an interval, like [1,3], which represents the set {1,2,3}, and an interval, which represents the step between each element. For instance, the strided interval 5[0,9] represents the set {0,4,9}. The idea in VSA is that once you can approximate program values in this way, you can then reason about (resolve) indirect jumps, and thus recover the CFG.

BAP has a partial implementation of VSA, but it needs some re-design before we can use it for CFG recovery. First, we need to change the type of CFG edges. Right now, CFG edges are of type bool option, since an edge can be an unconditional jump (None), or be the taken or non-taken edge of a conditional jump (Some true or Some false). However, we need more expressive edges for two reasons. First, we need to represent information about recovered indirect jumps. For instance, we might find that jmp (%eax) goes to address 10 when %eax is 30, and to address 20 when %eax is 100. Obviously we can’t represent this using true and false; we need expression types. The second reason we need more expressive edges is that some abstract interpretation algorithms, like VSA, are defined for both program statements and edge conditions.

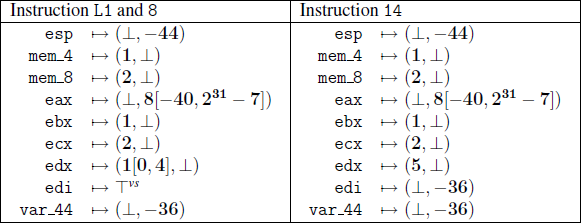
This is best understood with an example. In the above program, it’s easy to see that x can only contain the values {0,1,2} coming into BB 1. We know this, because x starts with value 0, and if it had a value above 3, control would transfer to BB 2. VSA can actually determine this. BAP’s VSA does not take edge conditions into account (after all, edges have no conditions!), and so BAP would be forced to conclude that the range of x is [0, ∞] coming into BB 1.

Okay, so we want to add conditions to CFG edges. BAP’s VSA implementation uses the Single Static Assignment (SSA) form, so let’s convert our program to that and see what it looks like.

What’s this temp variable? Well, it’s a temporary variable introduced because BAP’s SSA form is three address code (TAC). TAC ensures that each expression has no subexpressions. Instead, subexpressions must be computed with separate assignments. This makes some analyses simpler. For instance, Strongly Connected Component Value Numbering (SCCVN) can easily identify common subexpressions, since each subexpression gets its own assignment.

Unfortunately, TAC comes back to bite us in VSA. The edge temp = false does not convey any information about x to VSA, since VSA can only relate edge conditions to data values syntactically, that is to temp. This is the major difference between abstract interpretation and a symbolic analysis like symbolic execution. Symbolic analysis can reason about the effect of an edge condition on a data value with symbolic constraints. Abstract interpretation typically does not involve constraint solving, and thus VSA does not know how an edge condition affects a data value in the general case.

So, to make a long story short, I am going to adjust BAP’s SSA representation so that TAC is not enforced by the type system. Instead, we’ll have an option to lift to TAC, which we will use with SCCVN. VSA, however, will use the non-TAC version of SSA. Once VSA is fixed, it should be straight-forward to use the resulting information to do CFG recovery.

Being a software security researcher in academia, I spend a fair amount of time talking to non-academic security researchers. These conversations are extremely valuable: academics should be aware of the problems that industry perceives as important. Yet, these conversations have also shown that industry researchers hold some fundamental misconceptions about the nature of academic security research.

1. The research you see is “new”

   Most people have never submitted a paper to an academic conference, and naturally have no idea what the timeline is like. Let’s take a look at the call for papers (CFP) at one of the highest regarded academic security conferences, IEEE Security and Privacy (which is also called “Oakland”).

   Research papers were due on November 16th, 2011. Ideally, the idea and proof of concept for research is completed at least a month before the due date, to allow enough time for writing and experiments. So, let’s say the research is from about mid-October. Based on my personal experience, it can easily take six months to produce research for a paper, so we’ll say that research started in mid-April, 2011. The Oakland 2012 conference actually met in May 2012. So the research presented there was an entire year old! This also assumes that the paper was accepted in the first conference it was submitted to. By the time you see and hear about this work, the researchers have probably started writing their next paper, or have moved on to another topic.

   This is one of the reasons that academia seems to struggle to keep pace with industry. It’s not that we are really behind, but it takes a long time for results to be disseminated. As a real world example, our group was criticized by some industry researchers when we released our paper on Automatic Exploit Generation for not handling defenses like DEP. At the time that AEG was published, I was already working on a separate paper on Exploit Hardening, or how to transform exploits so that they bypass defenses.

2. Academic prototypes are supposed to solve industry problems

   If you’ve been in the security community long enough, you’ve probably heard at least one person complain that an academic paper did not release their prototype, or that a released prototype did not solve industrial problems (e.g., it sucked).

   Industry focuses on tangible products – after all, that is why it is industry! So, it is unsurprising that in industrial circles, prototypes are often more important than the ideas employed in them. For example, there are dozens and dozens of fuzzers available, and yet there are few novel ideas employed in each of them. It is natural for industry researchers to transfer their expectations to academia as well: if this group’s prototype is so crappy, what use is the paper?

   Unlike industry, academia values ideas over implementations. Here is a quote from the Oakland Call For Papers (CFP), which describes the type of papers they solicit:

   Since 1980, the IEEE Symposium on Security and Privacy has been the premier forum for computer security research, presenting the latest developments and bringing together researchers and practitioners. We solicit previously unpublished papers offering novel research contributions in any aspect of computer security or privacy. Papers may present advances in the theory, design, implementation, analysis, verification, or empirical evaluation of secure systems.

   Note the phrase novel research contributions. To write an academic paper, you must discover something new. Also note that nothing is mentioned about a prototype in the CFP. Academic prototypes usually support the novel contribution that is the basis of the paper, whereas in industry the prototype often is the contribution. Even academic systems papers must have a novel contribution, for instance a new design technique that enabled the system.

   While the ideas and contributions of an academic paper may be widely applicable, the prototypes are often of limited use outside of the paper’s experiments. These prototypes are often written or modified on tight deadlines, and the code is often unmaintainable (or even unusable!) by anyone other than the creator. It’s usually not just a matter of releasing the code; researchers would need to spend significant time to clean and fix prototypes.

   I have yet to hear a reasonable argument why academics should spend their time to create stable prototypes for industry. Is industry going to pay us for our time? Are they going to give us stock options to share the profits? No, of course not. It’s industry’s job to productize research. On the other hand, it’s academia’s responsibility to undertake more risky ideas and directions that may or may not lead to industry improvements. Because academia is not profit driven, we can think more outside the box, which leads to larger discoveries.

3. Academics do not understand exploits

   Many industry researchers think that because academics target stack-based buffer overflows, and do not consider defenses, that this constitutes our entire knowledge of exploits.

   Academics keeps their jobs by writing many papers. In general, it is preferable to write three incremental papers than one super novel paper that contains ten years of research. There’s a saying in academia that “Deans can’t read, but they can count”, meaning that deans do not understand the significance of papers, but can count how many of them are published in reputable conferences.

   Academic researchers that value their jobs target a piece of a larger problem that is significant enough to be accepted by a reputable conference. For example, research in automatic exploitation is very new, and so it makes a lot more sense to target the low hanging fruit first: stack exploits, small or medium sized programs, and limited or no defenses. We will get to the harder cases in time.

   These incremental papers are accepted because they contain novel research contributions. In other words, there is enough information there to raise the bar on public knowledge each time. Industry may not be able to convert these papers to products without more research, but that is not the goal of academic research. At the end of the day, we academics want to understand the world a little more.

I’ve had a lot going on lately, so sorry for the lack of posts.

Today I’d like to post about an interesting security vulnerability that was just discovered in MySQL. The problem is extremely serious: by simply attempting to login ~256 times, the user gains access. From a practical point of view, it’s amazing that such a serious vulnerability is present in such a popular software package. It’s even more astounding when you consider how simply the “exploit” is.

So, here’s the vulnerable C code:

1
2
3
4
5
6
7

my_bool
check_scramble(const char *scramble_arg, const char *message,
               const uint8 *hash_stage2)
{
...
  return memcmp(hash_stage2, hash_stage2_reassured, SHA1_HASH_SIZE);
}

Did you spot the bug? Here’s another hint, the fixed code:

1
2
3
4
5
6
7
8
9

#define test(a)         ((a) ? 1 : 0)

my_bool
check_scramble(const char *scramble_arg, const char *message,
               const uint8 *hash_stage2)
{
...
  return test(memcmp(hash_stage2, hash_stage2_reassured, SHA1_HASH_SIZE));
}

What’s going on is that C does not have a native bool type, and so MySQL uses char. The return value of memcmp, which is non-zero for non-matching comparisons, is cast using truncation to a char. For example, a return value of 0x100 would be truncated to 0, which is interpreted as a successful comparison. Oops! The real problem is that bools do not behave like integers, and as programmers we expect a boolean cast (0 maps to false, anything else maps to true), which C doesn’t provide. I found this bug very interesting, because at first glance it looked correct. Another argument for program analysis and verification.

If you found this interesting, you might enjoy this quiz on C integers. I only got 88%. (I guess you can tell I work on binaries!)

Good news: we just opened the BAP nightly reports to the public. Bad news: the pcmpistri instruction has been wrong for the past few days, even though I’ve been trying to fix it.

pcmpistri has the worst documentation of any instruction I’ve seen in the Intel manual. pcmpistri is one of the newer SSE string instructions. It can perform a variety of operations, including strcmp, substring searching, and character set and range matching. There’s an excellent blog post that covers the uses of pcmpistri and its related instructions.

This purpose of this blog post is to share some of the gotchas that I ran into when trying to fix our modeling of pcmpistri in BAP. To the best of my knowledge, these gotchas are undocumented. (To be fair, the documentation is so poorly written it’s hard to tell if these issues are addressed.) The above linked blog post avoids discussing these gotchas by discussing things at an abstract string level.

Strings in registers are reversed

pcmpistri can take both of its input strings in registers. In memory, strings are usually stored with later (farther right) characters being stored at higher memory addresses. It is unclear how strings should be represented while they are in a register. I personally think that “abcd” should be stored as 0x61626364. More generally, the rightmost character of a string would be stored in the least significant byte of the register. There is no deep reason for this convention. However, numbers are stored in the correct byte order while in registers, and it seems weird for strings to be in reverse order.

For example, what do you think

1

pcmpistri $0xc, %xmm1, %xmm2

should return when %xmm1 == 0x6b6579206b6579206b6579206b657920 and %xmm2 == 0x6b657900000000000000000000000000? pcmpistri $0xc, %xmm1, %xmm2 is supposed to return the least significant byte index of %xmm1 that contains the substring in %xmm2. Note that %xmm2 is “key” and %xmm1 is “key key key key “.

You might, like me, think that the result should be 3 (the least significant index is 0). But you’d be wrong. In fact, pcmpistri interprets the strings backwards. So, %xmm2 == 0x6b657900000000000000000000000000 == "", because it starts with a null byte.

Why interpret strings like this? Consider the following snippet:

1
2
3
4
5

    movdqu substr, %xmm1
    movdqu str, %xmm2
    pcmpistri $12, %xmm2, %xmm1
substr: .ascii "key\0"
str:    .ascii "key key key\0"

When substr and str are copied to %xmm1 and %xmm2, they are reversed. movdqu does not know that it is copying a string, and will reverse the byte order of the string, since the x86 is a little endian machine. So, operating on reversed strings does make sense on a little endian machine, but this may not be intuitive. It certainly wasn’t what I was expecting.

Output selection is confusing

The immediate byte that is the first argument to pcmpistri is called the imm8 control byte. This is documented in section 4.1 in Volume 2 of the Intel Manual. For pcmpistri, the sixth bit of this byte controls the Output Selection. The value 12 denotes that, among other things, that the least significant index should be returned. In contrast, 76 would denote that the most significant index should be returned.

Least significant and most sigificant here apply to the little endian (reversed) string representation. So, least significant means the leftmost character of the string, and most significant means the rightmost character of the string. This is exactly the opposite of my intuition for what the least and most sigificant bytes of a string are.

As an example, the above code for pcmpistri $12, %xmm2, %xmm1, which specifies the least significant output setting, returns 0 in %ecx. On the other hand, the most significant output setting, pcmpistri $76, %xmm2, %xmm1 returns 8 in %ecx.

I am busy writing papers these days, but I wanted to share two surprising statistics.

A trace of the hello world program written in C executes 500,000 BAP IL statements. That’s a lot. But a trace of the hello world program written in C++ executes 7,500,000 BAP IL statements.

Wow. Computers are amazing, and amazingly complex.

Lately, I’ve been thinking about binary instrumentation. Binary instrumentation is awesome. Dynamic binary instrumentation (DBI) frameworks like Pin allow you to effectively insert your own code in between a binary program’s instructions. Such a capability is obviously very powerful. In our research, we use PIN to record execution traces that we can then analyze with BAP.

PIN is a great tool. It has a nice API that makes many things easy, and I’ve never found an instruction it can’t handle. (It’s made by Intel – it figures they could actually completely model their own architecture.) PIN works by reading binary code, adding the user’s specified instrumentation, and then Just In Time (JIT) compiling the whole thing. This got me thinking: BAP can understand binary code and allow users to modify it using a visitor interface. But, the BAP interpreter is really slow.

How slow? Let’s create a simple program and find out:

1
2
3
4
5
6
7
8

ctr:u32 := 100000:u32
accum:u32 := 0:u32
label begin
ctr:u32 := ctr:u32 - 1:u32
accum:u32 := accum:u32 + ctr:u32
cjmp ctr:u32 == 0:u32, "end", "begin"
label end
halt accum:u32

This program computes the sum of the first 100,000 numbers. Shouldn’t take too long to execute, right?

1
2
3
4
5

ed@ed-ThinkPad-T510:/tmp$ time ileval -il loop.il -eval

real                      0m26.773s
user                      0m26.658s
sys                       0m0.040s

Ouch! Almost 30 seconds. That is only ~4000 loop iterations per second. That got me thinking: How difficult is it to do JIT? It’s surprisingly easy! There are plenty of JIT frameworks to choose from these days. I chose to use LLVM, because I was already familiar with it, and because there is an OCaml LLVM interface. Because BAP and LLVM are fairly well designed, it only took me about 48 hours to implement a BAP IL to LLVM IL converter. Let’s re-run the JIT version of the code and see how long it takes.

1
2
3
4
5

ed@ed-ThinkPad-T510:~/f11/llvm$ time ./utils/codegen -il /tmp/loop.il -exec

real    0m0.015s
user    0m0.004s
sys     0m0.008s

Holy smokes that was fast! Let’s see how this got converted to LLVM IL:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

define i32 @0() {
allocs:
  store i32 100000, i32* @ctr, align 4
  store i32 0, i32* @accum, align 4
  br label %BB_1

BB_1:                                             ; preds = %BB_1, %allocs
  %load_var_ctr = load i32* @ctr, align 4
  %-_tmp = add i32 %load_var_ctr, -1
  store i32 %-_tmp, i32* @ctr, align 4
  %load_var_accum = load i32* @accum, align 4
  %"+_tmp" = add i32 %load_var_accum, %-_tmp
  store i32 %"+_tmp", i32* @accum, align 4
  %"==_tmp" = icmp eq i32 %-_tmp, 0
  br i1 %"==_tmp", label %BB_2, label %BB_1

BB_2:                                             ; preds = %BB_1
  %load_var_accum3 = load i32* @accum, align 4
  ret i32 %load_var_accum3
}

And here is the x86 assembly:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# BB#0:                                 # %allocs
        movl    $100000, ctr            # imm = 0x186A0
        movl    $0, accum
        .align  16, 0x90
.LBB0_1:                                # %BB_1
                                        # =>This Inner Loop Header: Depth=1
        movl    ctr, %eax
        decl    %eax
        movl    %eax, ctr
        addl    %eax, accum
        testl   %eax, %eax
        jne     .LBB0_1
# BB#2:                                 # %BB_2
        movl    accum, %eax
        ret

One small issue is how to deal with memory: Sometimes we don’t want a bad memory read or write to crash our whole evaluation. There are two modes in the BAP to LLVM conversion. The first mode does no sandboxing: a memory write in the BAP IL is translated directly to a LLVM memory write. The second mode replaces all memory operations in the BAP IL with calls to C++ functions that set and read a std::map object.

Look for the LLVM JIT code to appear in a new BAP release coming soon!